Introdução
O QUE É GRAFO?
A palavra “grafo” é um neologismo derivado da palavra graph em inglês. Ela foi usada pela primeira vez no sentido que nos interessa pelo matemático inglês James Joseph Sylvester.
A teoria dos grafos é um ramo da matemática que estuda as relações entre os objetos de um determinado conjunto. Para tal são empregadas estruturas chamadas de grafos, G(V,W), onde V é um conjunto não vazio de objetos denominados vértices e W é um conjunto de pares não ordenados de V, chamado arestas.
Uma aresta como {v, w} será denotada simplesmente por vw ou por wv . Diremos que a aresta vw incide em v e em w e que v e w são as pontas da aresta. Se vw é uma aresta, diremos que os vértices v e w são vizinhos ou adjacentes. De acordo com nossa definição, um grafo não pode ter duas arestas diferentes com o mesmo par de pontas (ou seja, não pode ter arestas “paralelas”). Também não pode ter uma aresta com pontas coincidentes (ou seja, não pode ter “laços”). Há quem goste de enfatizar esse aspecto da definição dizendo que o grafo é “simples”. Muitas vezes é conveniente dar um nome ao grafo como um todo. Um grafo pode ter vértices rotulados por grau, isso significa quantas arestas chegam no vértice.
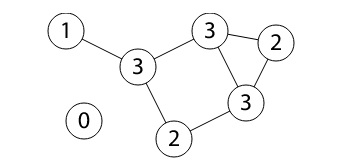
Exemplo 1: Grafo simples
Dependendo da aplicação, arestas podem ou não ter direção, pode ser permitido ou não arestas ligarem um vértice a ele próprio (laços) e vértices e/ou arestas podem ter um peso (numérico) associado. Se as arestas têm uma direção associada (indicada por uma seta na representação gráfica) temos um grafo direcionado, grafo orientado ou digrafo. Um exemplo simples é a estrutura de ligações de um web site que são representadas por um dígrafo: os vértices são os artigos do web site, existe uma aresta do artigo A para o artigo B se e somente se A contém um link para B (A →B). Um grafo com um único vértice e sem arestas é conhecido como o grafo trivial.
Grafo Simples: cada aresta conecta dois vértices diferentes {u, v}. Multigrafos: arestas multiplas: várias arestas conectadas ao mesmo vértices. Laços: Arestas que conectam um vértice a sí mesmo.
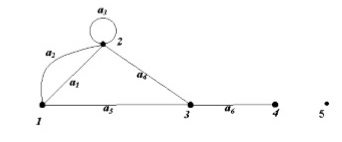
Exemplo 2: Grafo Completo
Onde a3 é um laço, 5 é um grafo trivial, a4 é uma aresta.
Digamos que os vértices de nosso grafo orientado (dígrafo) são 0, 1, 2, 3, 4, 5, 6, 7, 8 e os arcos são a, b, c, d, e, f, g, h, i, j. Então a seguinte tabela o define:
|
ponta inicial |
|
0 |
0 |
2 |
6 |
6 |
6 |
1 |
1 |
3 |
8 |
|
arco |
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
|
ponta final |
|
0 |
2 |
6 |
0 |
2 |
4 |
3 |
3 |
7 |
5 |
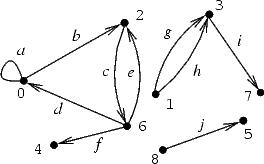
Exemplo 3: Grafo Orientado
Exemplo 4:
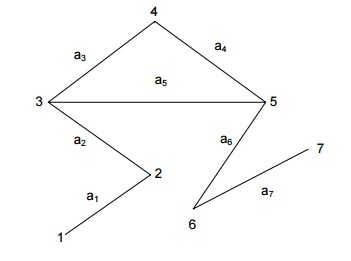
Considere o grafo e responda as seguintes perguntas:
a) O grafo é simples?
b) O grafo é completo?
c) O grafo é conexo?
d) É possível encontrar dois caminhos do nó 3 para o nó 6?
e) É possível encontrar um ciclo?
f) É possível encontrar um arco cuja remoção transforma o grafo em um grafo acíclico?
g) É possível encontrar um arco cuja remoção transforma o grafo em um grafo não-conexo?
SOLUÇÃO DO EXEMPLO 4
a) Sim.
b) Não, os nós 5 e 7, por exemplo, não são adjacentes.
c) Sim.
d) Sim, 1º caminho: 3 – A5 – 5 – A6 – 6 e 2º caminho: 3 – A3 – 4 – A4 – 5 – A6 – 6.
e) Sim: 3 – A3 – 4 – A4 – 5 – A5 – 3.
f) Sim: A5.
g) Sim: A7, por exemplo.