Desenvolvimento

Subgrafos

Em teoria dos grafos, um subgrafo de um grafo G é um grafo cujo conjunto de vértices é um subconjunto do conjunto de vértices G e o conjunto de arestas é um subconjunto do conjunto de arestas de G1, ou seja, cuja relação de adjacência é um subconjunto de G restrita a esse subconjunto.

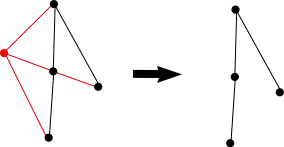
Exemplo 1: Subgrafo

No grafo acima, aparte em preto é um subgrafo do grafo maior, pois está contido nele, compartilhando os mesmos vértices e arestas. A parte em vermelho, nesse caso, é chamada de grafo complementar, que consiste basicamente no grafo maior menos o subgrafo.

Grafos conexos

Já dissemos que um grafo é conexo se não tem cortes vazios.  Eis uma fato básico importante, que estabelece a relação entre essa definição e a existência de caminhos que ligam pares de vértices:

Fato:  Um grafo é conexo se e somente se, para cada par  s t  de seus vértices, existe um caminho com origem  s  e término  t. Em virtude da simetria dos grafos, a existência de um caminho de s a t equivale à existência de um caminho de t a s.  Portanto, um grafo é conexo se e somente se quaisquer dois de seus vértices são ligados por um caminho.

Teorema do aperto de mão

Seja E o número de arestas do grafo, r o grau e V o número de nós(vértices), pode-se apresentar a relação:

2*E=r*V

Exemplo: Quantas arestas possui um grafo de grau 4 com 5 vértices?

2*E=4*5

E=10 arestas

Tipos de grafos

Grafo simples é um grafo não direcionado, sem laços e que existe no máximo uma aresta entre quaisquer dois vértices (sem arestas paralelas). No grafo de exemplo, (1, 2, 5, 1, 2, 3) é um caminho com comprimento 5, e (5, 2, 1) é um caminho simples de comprimento 2.

Grafo completo é o grafo simples em que, para cada vértice do grafo, existe uma aresta conectando este vértice a cada um dos demais. Ou seja, todos os vértices do grafo possuem mesmo grau. O grafo completo de n vértices é frequentemente denotado por Kn. Ele tem n(n-1)/2 arestas (correspondendo a todas as possíveis escolhas de pares de vértices).

• Grafo nulo é o grafo cujo conjunto de vértices é vazio.
• Grafo vazio é o grafo cujo conjunto de arestas é vazio.
• Grafo trivial é o grafo que possui apenas um vértice e nenhuma aresta.
• Grafo regular é um grafo em que todos os vértices tem o mesmo grau.

Multigrafo é um grafo que permite múltiplas arestas ligando os mesmos vértices (arestas paralelas). Laço (loop) num grafo ou num digrafo é uma aresta e em E cujas terminações estão no mesmo vértice. Pseudografo é um grafo que contém arestas paralelas e laços.